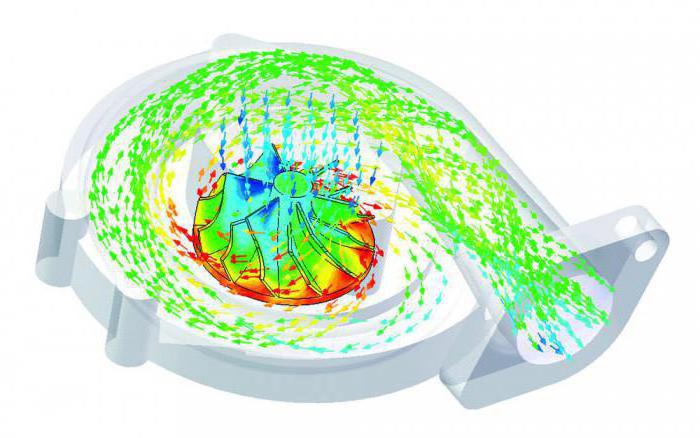
Детермінована модель: визначення. Основні типи факторних детермінованих моделей

Моделювання є одним з найважливішихінструментів в сучасному житті, коли хочуть передбачити майбутнє. І це не дивно, адже точність такого способу досить велика. Давайте ж в рамках даної статті розглянемо, що собою являє детермінована модель.

Загальна інформація

Детерміновані моделі систем мають туособливість, що можуть досліджуватися аналітично, якщо вони є досить простими. В протилежному випадку при використанні значної кількості рівнянь і змінних для цієї мети можуть бути задіяні електронно-обчислювальні машини. Причому допомога ЕОМ, як правило, зводиться виключно до їх вирішення і знаходженню відповідей. Через це доводиться міняти системи рівнянь і використовувати іншу дискретизацию. А це влёчет за собою підвищену небезпеку похибки при розрахунках. Всі типи детермінованих моделей характеризуються тим, що знання параметрів на певному досліджуваному інтервалі дозволяє нам повністю визначити динаміку розвитку за кордоном відомих показників.

Особливості

Детерміновані математичні моделі недозволяють одночасно визначати вплив безлічі чинників, а також не враховують їх взаємозамінність в системі зворотних зв'язків. На чому ж вибудовується їх функціонал? Він базується на математичних закономірностях, які описують фізико-хімічні процеси об'єкта. Завдяки цьому досить точно передбачається поведінку системи.

Для будівництва також використовуються узагальненірівняння теплового і матеріального балансів, які визначаються Макрокінетика процесу. Для більшої точності прогнозування детермінована модель повинна володіти максимально можливою кількістю вихідної інформації про минуле даного об'єкту. Вона може бути застосована щодо тих технічних завдань, де допускається по тій або іншій причині знехтувати реально існуючими флуктуаціями значень параметрів і результатами їх вимірювання. Також одним з показань до використання є те, що випадкові помилки можуть надати несуттєвий вплив на кінцевий розрахунок системи рівнянь.

Види детермінованих моделей

Вони можуть бути не / періодичними. Обидва види можуть бути безперервним у часі. Також вони представляються у вигляді послідовності дискретних імпульсів. Описуватися вони можуть за допомогою зображення по Лапласа або завдяки інтегралу Фур'є.

Детерміновані факторні моделі маютьпевні зв'язки між вхідними і вихідними параметрами процесу. Задаються моделі за допомогою логічних, диференціальних і алгебраїчних рівнянь (хоча можуть використовуватися і їх рішення, представлені як функція часу). Також в якості основи для розрахунків можуть виступати експериментальні дані, які були отримані в натуральних умовах або при прискорених корозійних випробуваннях. Будь-яка детермінована модель передбачає певне усереднення характеристик системи.

Використання в економіці

Давайте розглянемо практичне застосування. Для цього підійдуть детерміновані моделі управління запасами. Слід зазначити, що вони формалізовані в класі задач лінійного програмування.

Так, для розрахунків необхідно визначити наступніпоказники: витрати ресурсів і випуск продукції за допомогою різних способів виробництва, кожен з яких має свою інтенсивність; змінні, що описують всі характеристики в процесах, що відбуваються (у тому числі і сировину з матеріалами). Все повинно бути опрацьовано. Кожен окремий ресурс, товар, послуга - все це вноситься в матеріальний баланс.

Також для повноти рішень необхідно датиоб'єктивну оцінку якості прийнятих рішень. Таким чином, детерміновані економічні моделі ідеально підходять для опису процесів, від яких залежить початковий стан системи. При роботі з електронно-обчислювальними машинами необхідно враховувати, що комп'ютери можуть працювати тільки з фіксованими факторами.

побудова моделей

За способом представлення основних параметрів що відбуваються технологічних процесів можна розділити два типи:

1. Апроксимаційні моделі. У них окремі виробничі одиниці представлені як сукупність фіксованих векторів граничних варіантів їх функціонування.
2. Моделі зі змінними параметрами. В даному випадку встановлюються певні діапазони варіювання, і для відповідності векторах граничних варіантів вводяться додаткові рівняння.

Ці детерміновані факторні моделі дозволятьприменяющему їх людині визначити вплив конкретних положень на окремі характеристики. Але отримати для кривих розподілу розрахункові вирази не вийде. Якщо ж буде прораховуватимуться динамічна оптимізація безперервних виробництв, то не слід враховувати вірогідну природу інформації про те, як протікають технологічні процеси.

факторний моделювання

Зв'язок із цього можна було побачити на протязівсій статті, але що це таке, ми поки не обговорювали. Факторний моделювання має на увазі, що виділяються основні положення, для яких необхідно кількісне зіставлення. Для виконання поставлених цілей дослідженням виробляють перетворення форми.

Якщо жорстко детермінована модель має більшедвох чинників, то вона називається багатофакторної. Її аналіз може здійснюватися за допомогою різних прийомів. Як приклад наведемо математичну статистику. В цьому випадку вона розглядає поставлені завдання з точки зору заздалегідь встановлених і опрацьованих апріорних моделей. Вибір серед них здійснюється по змістовному поданням.

Для якісного побудови моделі необхідновикористовувати теоретичні і експериментальні дослідження сутності технологічного процесу і його причинно-наслідкових зв'язків. Саме в цьому і полягає головна перевага розглянутих нами суб'єктів. Моделі детермінованого факторного аналізу дозволяють здійснювати точне прогнозування в багатьох сферах нашого життя. Завдяки їх якісними параметрами і універсальності вони і отримали таке широке поширення.

Кібернетичні детерміновані моделі

Вони представляють для нас інтерес завдякизаснованим на аналізі перехідних процесів, які виникають при будь-яких, навіть самих незначних змінах агресивних властивостей зовнішнього середовища. Для простоти і швидкості розрахунків існуючий стан справ замінюється спрощеною моделлю. Важливим є те, щоб вона задовольняла всіх основних запитам.

Від єдності всіх необхідних параметрів залежитьпрацездатність системи автоматичного управління і ефективність прийнятих нею рішень. При цьому необхідно вирішити таке завдання: чим більше буде зібрано інформації, тим вище ймовірність помилки і значніше термін обробки. Але якщо обмежити збір своїх даних, то можна розраховувати на менш надійний результат. Тому необхідно знайти золоту середину, яка дозволить отримати інформацію достатньої точності, і одночасно це не буде надмірно ускладнено зайвими елементами.

Мультиплікативна детермінована модель

Вона будується за допомогою поділу факторів наїх безліч. Як приклад можна розглянути процес формування обсягу виробленої продукції (ПП). Отже, для цього необхідно мати робочу силу (РС), матеріали (М) і енергію (Е). В такому випадку фактор ПП можна розбити на безліч (РС; М; Е). Такий варіант відображає мультиплікативний вигляд факторной системи і можливість її поділу. В цьому випадку можна використовувати такі методи перетворення: розширення, формальне розкладання і подовження. Перший варіант знайшов широке застосування в аналізі. Він може використовуватися для того, щоб вирахувати ефективність діяльності працівника, і так далі.

При подовженні одне значення замінюється іншимифакторами. Але в кінцевому підсумку повинно вийти те ж саме число. Приклад подовження був розглянутий нами вище. Залишилося тільки формальне розкладання. Воно передбачає використання подовження знаменника вихідної факторної моделі завдяки заміні одного або декількох параметрів. Розглянемо такий приклад: ми розраховуємо рентабельність виробництва. Для цього сума прибутку ділиться на розмір витрат. При мультиплікації замість єдиного значення ділимо на підсумовані витрати на матеріал, персонал, податки і так далі.

ймовірності

О, якби все йшло саме так, як задумано! Але таке буває рідко. Тому на практиці часто разом використовуються детерміновані і імовірнісні моделі. Що можна сказати про останні? Їх особливість в тому, що вони враховують ще й різні ймовірності. Візьмемо, наприклад, наступне. Є дві держави. Відносини між ними дуже погані. Третя сторона вирішує, чи інвестувати в підприємства однієї з країн. Адже якщо розгориться війна, то прибуток дуже постраждає. Або можна привести в приклад побудову заводу в зоні з високою сейсмічною активністю. Адже тут діють природні чинники, які точно врахувати не можна, можна це зробити тільки приблизно.

висновок

Нами було розглянуто, що собою представляютьмоделі детермінованого аналізу. На жаль, але щоб повноцінно розібратися в них і вміти застосовувати на практиці, слід дуже добре повчитися. Теоретичні основи вже є. Також в рамках статті були представлені і окремі прості приклади. Далі краще йти по шляху поступового ускладнення робочого матеріалу. Можна трохи спростити собі задачу і почати вивчення програмного забезпечення, яке може проводити відповідне моделювання. Але яким би вибір не був, розуміти основи і вміти дати відповідь на питання про те, що, як і чому, все ж необхідно. Слід навчитися для початку підбирати правильні вхідні дані і вибирати потрібні дії. Тоді програми зможуть успішно виконувати свої завдання.

</ P>